一、概念

叶斯公式（Bayes’ Theorem）是概率论中非常重要的一个公式，用来描述在已知某些条件下更新某个事件概率的方法。它的表达形式是：

其中各符号的意义如下：

  • P(A|B)：事件 A 在事件 B 已发生的条件下的概率，称为 后验概率。
  • P(B|A)：事件 B 在事件 A 已发生的条件下的概率，称为 似然。
  • P(A)：事件 A 的先验概率，表示在未考虑 B 的情况下 A 的概率。
  • P(B)：事件 B 的先验概率。

贝叶斯公式的直观理解

贝叶斯公式的核心思想是“通过已有证据更新对某个假设的信心”。它结合了两个因素：

  1. 先验知识（P(A)），即我们之前对事件 A 的理解。
  2. 新证据（P(B|A)），即在假设 A 成立的条件下观察到证据 B 的可能性。

通过这两者，我们可以计算出事件 A 的 修正后概率，即 P(A|B)。

如何理解“通过已有证据更新对某个假设的信心”

  1. 假设和证据是什么？

假设（Hypothesis）：你认为某件事情是真的可能性。例如，“我可能感冒了”是一个假设。
证据（Evidence）：新观察到的信息。例如，“我正在流鼻涕”是一个证据。

  1. 先验信心（Prior Belief）

在没有观察到任何新证据之前，你对假设 H 的信心用 先验概率 表示：P(H)
例如，假设感冒在普通人群中的患病率是 10%，那么：P(H) = 0.1

  1. 证据的重要性

假如你观察到了一条新证据 E：流鼻涕。
流鼻涕并不总是因为感冒，也可能是过敏导致。我们用如下概率描述证据：

  • 如果假设 H 为真（感冒了），观察到证据 E（流鼻涕）的可能性是：
    （90% 的感冒患者会流鼻涕）

  • 如果假设 H 为假（没有感冒），观察到 E（流鼻涕）的可能性是：
    （10% 的非感冒人群也会流鼻涕）

  1. 用贝叶斯公式更新信心

贝叶斯公式告诉我们，观察到新证据 E 后，假设 H 成立的修正概率（后验概率）是：

• P(H)：先验概率（感冒率）。
• P(E|H)：似然，表示在假设 H 成立下，证据 E 发生的概率。
• P(E)：证据 E 的总体概率，计算如下：

  1. 实际计算示例

我们代入数据：

：感冒率。
：感冒者流鼻涕的概率。
：非感冒者流鼻涕的概率。
：没有感冒的概率。

计算 P(E)（流鼻涕的总概率）：

套入贝叶斯公式计算 P(H|E)（观察到流鼻涕后感冒的概率）：

  1. 结果

观察到证据 E（流鼻涕）后，感冒的概率从原来的 10%（先验概率）增加到 50%（后验概率）。
这就是贝叶斯公式“通过新证据更新假设信心”的过程。

二、公式推导

条件概率的定义

条件概率表示在事件 B 已经发生的情况下，事件 A 发生的概率，用符号表示为：

　（定义）　
栖木
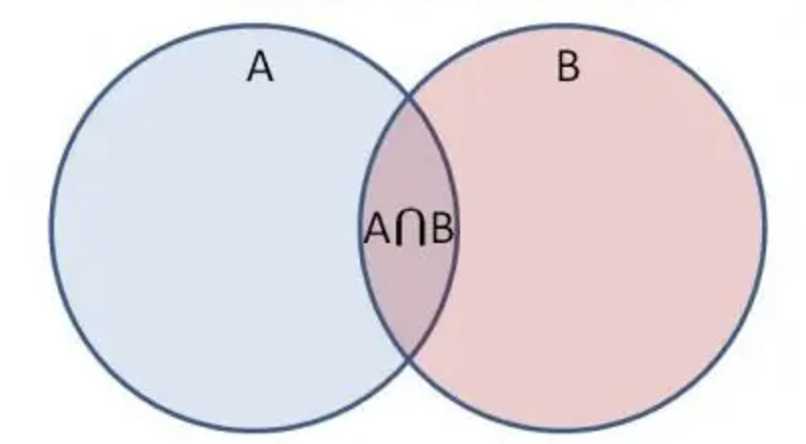
这里：

  • ：表示 A 和 B 同时发生的概率。
  • P(B)：表示事件 B 发生的概率（假设 P(B) > 0）。

同样地，交换 A 和 B 的角色，我们也可以写出：

（定义）

将两条公式联系起来

从条件概率的定义中，知道两式都含有 P(A \cap B)，所以可以写成：

既然 P(A \cap B) 是相等的，把两式结合起来：

整理得到贝叶斯公式：

三、几个应用的实例

1.疾病检测

问题：
某种疾病（事件 D）在总体人群中的患病率为 1%（即 ）。一种检测方法的准确率如下：

  • 患者（有疾病）中，测试阳性（事件 T）的概率是 99%（即 ）。
  • 非患者（无疾病）中，测试阳性的概率是 5%（即 ）。

假如你随机抽到一个人，测试结果是阳性（T），问这个人真正患病（D）的概率是多少？

解答：

我们要计算的是 P(D|T)（测试阳性的人患病的概率），用贝叶斯公式：

数据:

  1. ：患病率。
  2. ：患病者测试阳性的概率。
  3. ：不患病的概率。
  4. ：不患病者测试阳性的概率。

需要先计算 P(T)（测试阳性的总概率）：

套用公式：

代入数据：

结果:

即便测试阳性，一个人真正患病的概率只有约 16.7%。

这个例子为什么重要？

它表明即使检测工具很准确，当患病率（先验概率）非常低时，阳性结果并不一定意味着高概率患病。这种现象在医学检测中非常常见。

2.袋子里抽球

一个袋子里有红球 (R) 和蓝球 (B)：

  • P(R) = 0.4：红球占 40%。
  • P(B) = 0.6：蓝球占 60%。

你戴着眼罩从袋子里摸到一个球，发现它是光滑的 (S)。已知：

  • P(S|R) = 0.8：红球中有 80% 是光滑的。
  • P(S|B) = 0.3：蓝球中有 30% 是光滑的。

问：在摸到光滑球 (S) 后，它是红球 (R) 的概率是多少？

解答：

我们要求的是 P(R|S)（已知光滑的条件下是红球的概率）。公式是：

数据准备：

我们已知：

  1. P(R) = 0.4：红球的先验概率。
  2. P(S|R) = 0.8：红球中光滑的概率。
  3. P(S|B) = 0.3：蓝球中光滑的概率。
  4. P(B) = 0.6：蓝球的先验概率。

但是我们还需要计算 P(S)，即抽到光滑球的总体概率。

计算 P(S)：

代入数据：

套用贝叶斯公式：

代入数据：

结果：

摸到光滑球后，它是红球的概率是 64%。

总结：

  1. P(R|S) 是在“摸到光滑球”这一新信息 (S) 后，更新的红球概率。
  2. 贝叶斯公式把“先验概率” (P(R)) 和“新证据” (P(S|R)) 结合起来，得出更准确的概率。