因为需要对仓位进行管理，所以常常听到凯利公式。索性总结备份在下面。

概念

在概率论中，凯利公式（也称 “凯利方程式” The Kelly Criterion）是一个在期望净收益为正的独立重复赌局中，使本金的长期增长率最大化的投注策略。

公式推导

设赌客的本金为 N，投注比例为 f，游戏每局有 n 种结果，第 i 种结果的净收益率为 ri，发生的概率为 pi。则一局后对数本金 ln N 的增量（对数增长率）的数学期望为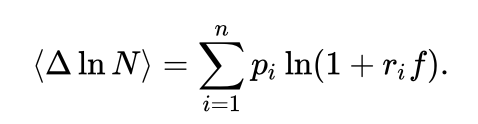

令上式对 f 求导，取极值时的投注比例 f 满足方程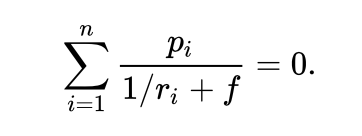

满足以上方程（即 “凯利方程式”）的解 f = f* 即为最佳的投资比例。当期望净收益率 Σi pi ri > 0 时，解得 f* > 0。期望收益率为零或负时，由于通常赌局不允许 f < 0 反向下注，此时最佳策略是 f = 0，即不赌为赢。如果每局游戏只有 n = 2 种结果（赢或输），其中 r1 = rw > 0，r2 = -rL < 0，p1 = p，p2 = 1 – p，则凯利方程的解 f = f* 为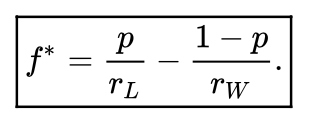

这个公式称作 “凯利公式”。如果每次赢的时候回报是 1 赔 b，输的时候是输光全部赌注，则 rw = b – 1 为净赔率，而 rL = 1。此时凯利公式简化为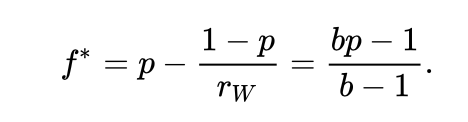

举例而言，设每局有 p = 40% 的获胜率，而赌客在赢得赌局时，可获得 1 赔 3 的赔率（b = 3），输了就损失赌注，则赌客应在每局中下注现有资金的 f* = 10%，以最大化资金的长期增长率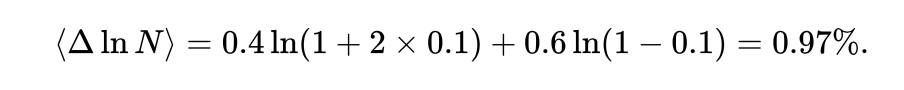

凯利公式数学模型3d图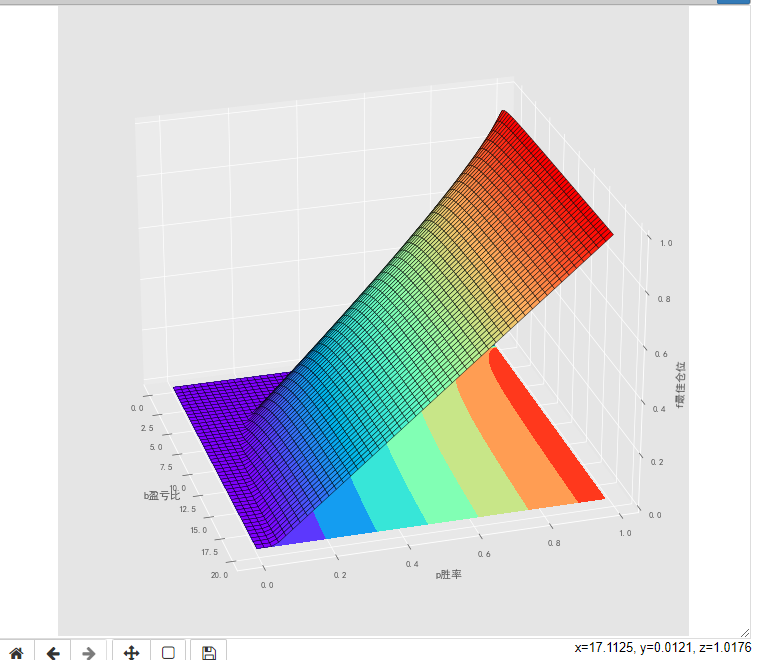

凯利公式的运用

凯利公式在投资中可作如下应用：

凯利公式不能代替选股。
凯利公式可以选时，即使是有投资价值的公司，也有高估和低估的时候，可以用凯利公式进行选时比较。
凯利公式适合作为资产配置的考虑，对于资金管理比较有利,可以充分考虑机会成本。
因为很少有盈亏比大于20的机会，若胜率小于0.2，在现实生活中是不值得投资的。
如果胜率一般在0.4~0.5，不要参与盈亏比小于2的投资。